イラストロジックを解く方法・道具
[ PR ]
「たまにはアナログもいいじゃないですか」― 管理人 F
ということで(笑)、今回はパソコンの話は一切ありません。純粋にイラストロジックについて話します。
実は、私が初めて買ったゲームは、「マリオのスーパーピクロス」でした。


スーパーファミコンの時代にしてはとても良くできたゲームで、それ以来ピクロスにハマって行くのでした。
そもそもイラストロジック(ピクロス)とは何なのでしょうか。
ルール
一番初歩的なものを紹介します。
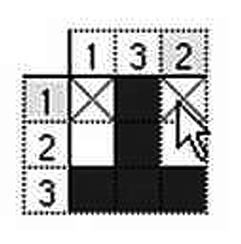
まず読み方ですが、左の数字が横の行、上の数字が縦の列です。
この局面では、中央の縦が■■■となり、3つ揃っているので数字と同じです。一番左の縦の列も、1つ■があるので数字と合っています。
残るは縦の列一番右の2に合うようにすればよく、答えは
132 1×■× 2×■■ 3■■■
で完成です。縦と横がクロス(Cross)し、ピクセル(Pixel)が塗りつぶされるのでピクロス(Picross)といわれます。
テクニック
交差法(Crossing Method)
次の問題を考えてみます。
4 □ □ □ □ □ □
これを解く方法として、交差法(Crossing Method)という方法を紹介しましょう。
例えば、上からびっしり塗りつぶすと仮定すると、
4 ▲ ▲ ▲ ▲ □ □
となります。逆に下からびっしり塗りつぶすと、
4 □ □ ▲ ▲ ▲ ▲
ですね。この2つを重ねてみるとどうなるでしょうか。
4 ▲ □ ▲ □ ★ ★ ★ ★ □ ▲ □ ▲
★を付けた2つが重なっていますね。つまりここは交差するので、塗りつぶすことが確定するのです。
4 □ □ ■ ■ □ □
これが交差法です。残りはこの方法ではわからないので、数字や周りとの関係から導きます。
充填法(Filling Method)
次のようなケースを考えます。
2 2 1 ■ ■ × □ □ × ■
空白の部分がまだ分かっていません。どうすれば分かるでしょうか。
よく数字を見てみると、残りは2マスであることが分かります。
ここで、より答えを導き出すには、既に分かっている数字を塗りつぶす事が重要です。
221■ ■ × □ □ × ■
実際は数字をにチェックマークを付けます。
ここで分かったのは、残りは2だけだということです。つまり、残り2マスかつ数字が2なので答えは自明です。
221■ ■ × ■ ■ × ■
これが充填法です。交差法でわからない場合は有効な方法です。
消去法(Elimination Method)
消去法(Elimination Method)は最も高度なテクニックです。次の例を考えてみます。
1 2 2 □ □ □ □ × ■ ■
上の4つが未定です。ここで、1つ仮定を立てることから始まります。
1
2
2
□
★
□
□
×
■
■
★のところが塗りつぶされるとしましょう。ではこれで解いていきます。
122× ★ × ■ × ■ ■
塗り終わりました。あれ?数が合っていませんね。これは矛盾しています。
つまり、最初の★で付けた仮定が誤っているということが分かりますので、実は×であったことが判明します。
122■ × < ■ ■ × ■ ■
これが消去法による解き方です。簡単なものは解けますが、大きくなってくるとツールによる補助が必要となってくるでしょう。
消去法が必要となってくるのは、交差法も充填法も歯が立たないケースです。その場合は最も協力なツールとなるでしょう。
テクニックの応用
交差法 + 充填法
次のようなケースを考えます。
3 3 □ □ □ □ □ □ □ □ □
何も情報がなくて難しいですね。こんな時はまず交差法を試します。
3 3 ◆ □ ◆ □ ★ ★ □ ◆ ★ ★ ◆ □ ★ ★ □ ◆ □ ◆
3ヶ所交差しましたね。ですが、本当にこれは正しいでしょうか。例えば、
3
3
■
■
■
□
□ <
□
■
■
■
かもしれません。すると、中央は間違いだとわかります。
そこで、中央以外の2つが正しいので塗りつぶします。
3 3 □ □ ■ □ □ □ ■ □ □
ここで、1つヒントを与えます。横の列との関係で真ん中が×だと確定したとしましょう。
3
3
□
□
■
□
×
□
■
□
□
ここで、充填法を考えます。
Q1. 上の4つに3が2つ入るでしょうか。 ⇒ NO
Q2. 下の4つに3が2つ入るでしょうか。 ⇒ NO
すると、上と下は独立した3があるとわかるので、初めて交差法が使えます。
3 3 □ ■ ■ □ × □ ■ ■ □
ここまで解けました。これで横の列が揃えば、十分解けるでしょう。
実践
2112 111132 46211221 4 □□□□□□□□ 22□□□□□□□□ 22□□□□□□□□ 8 □□□□□□□□ 2 □□□□□□□□ 22□□□□□□□□ 22□□□□□□□□ 4 □□□□□□□□
この問題を解いてみましょう。
手順1:最大数から解く
8に注目すると、この問題は8×8なので全て塗りつぶせます。
2112 111132 46211221 4 □□□□□□□□ 22□□□□□□□□ 22□□□□□□□□8■■■■■■■■ 2 □□□□□□□□ 22□□□□□□□□ 22□□□□□□□□ 4 □□□□□□□□
これがまず最初の一歩です。
手順2:次に1つの数字を解く
さて、今度は縦と横の両方に、4や6などの1つだけの数字があることがわかります。
そこで、既に塗りつぶされている8から推測して、可能な塗りつぶし範囲を交差法で当ててみます。
2112 111132 46211221 4 □□□□□□□□ 22□□□□□□□□ 22□■□□□□□□8■■■■■■■■ 2 □■□××××× 22□■□□□□□□ 22□□□□□□□□ 4 ×□□□■□□□
詳しく手順を説明すると、
- まず縦の列「4」の一番下のマスは届かないので X
- それから横をみると、交差法で1マス塗りつぶされる
- 横の列「2」は、既に1マス分かっているので、±1の範囲以外は X
ということになります。
手順3:隣が"X"になると終端がわかる
では、先程バツがいくつか付いたので、その周辺を見ていきましょう。
2112 111132 46211221 4 □□□□□□×□ 22□□□□□□■□ 22□■□□□□■□8■■■■■■■■ 2 □■□××××× 22□■□□□□□□ 22□□□□□□■□ 4 ×□□□■□□□
- 縦の列右から2列目、バツで2つに分かれているので、上は3と分かる。
- そこで3を上に向かって塗りつぶし、残りは交差法で下の1マスを割り出す。
2112 111132 46211221 4 □□□□□□×□ 22□□□□□□■□ 22□■□××□■□8■■■■■■■■ 2 □■□××××× 22□■□□□□□□ 22□□□□□□■□ 4 ×□□□■□□□
- 横の列上から3行目、2マス塗りつぶされているので、それぞれ±1以外は X
2112 111132 46211221 4 □□■■□□×× 22□□□□□□■□ 22□■□××□■□8■■■■■■■■ 2 □■□××××× 22□■□□□□□□ 22□□□□□□■□ 4 ×□□□■□□□
- 横:一番上の行、右から二番目が既に X なので、一番右も X
- すると、6マスが残るので交差法で2マス塗る
手順4:端の数字はヒント
2112111132 46211221 4 □□■■□□×× 22□□■×□□■□ 22□■×××□■□8■■■■■■■■ 2 □■□××××× 22□■□□□□□□ 22□□□□×□■□ 4 ×□□□■□□□
- 上端と下端を見ると、一番上・下の数字とわかるので、塗ってバツを付ける
2112111132 462111221 4 ×□■■□□××22×■■××□■□ 22□■××××■□8■■■■■■■■ 2 □■□××××× 22□■□□□□□□ 22□□□□×□■□ 4 ××□□■□□□
- 横の列上から2行目、左の端が X なので2と判明。
- するとバツが分かるので、縦横それぞれを塗りつぶす。
2112111132 46211221 4 ×□■■■□××22×■■××□■□ 22□■××××■□8■■■■■■■■2■■□×××××22■■□□□□□□ 22□□□□×□■□ 4 ××□□■■□□
- 先程のヒントにより縦横の4がそれぞれ塗れる。
手順5:ラストスパート
211211113246211221 4 ×□■■■□××22×■■××□■□22■■××××■■8■■■■■■■■2■■□×××××22■■□□□□□□ 22×□■□×□■□ 4 ××□□■■□□
- 上から3行目横:2・2が確定
- 左から1列目縦:4が確定
- 下から2行目横:4が確定したことにより左の2が交差法で一部確定
2112111132462112214××■■■■××22×■■××■■□22■■××××■■8■■■■■■■■2■■□×××××22■■□□□×□□22×■■□×■■□ 4 ××□□■■×□
- 右から3列目縦:充填法により2・1・2が確定
- 上から1行目横:それにより4が確定
- 上から2列目縦:それにより6が確定
2112111132462112214××■■■■××22×■■××■■□22■■××××■■8■■■■■■■■2■■××××××22■■×□□×□□22×■■□×■■□4××■■■■××
- 左から3列目縦:充填法により2・1・2が確定
- 下から1行目横:それにより4が確定
2112111132462112214××■■■■××22×■■××■■×22■■××××■■8■■■■■■■■2■■××××××22■■××××■■22×■■××■■×4××■■■■××
- 2つの1・1・1縦:自明で確定
- 下から2番目横:自明で2・2が確定
- 右から2列目縦:充填法により3・2が確定
- 最後に右から1列目縦:2・1が確定し 終了
2112 111132 46211221 4 ・・■■■■・・ 22・■■・・■■・ 22■■・・・・■■ 8 ■■■■■■■■ 2 ■■・・・・・・ 22■■・・・・■■ 22・■■・・■■・ 4 ・・■■■■・・
まとめ
どうですか?(笑) 少し早足でしたが、雰囲気は分かってもらえたかと思います。
ポイントは掴んでいるので、懸賞付きの雑誌にトライしたり、ネットの問題を解いてみてくださいね。
日本文芸社
売り上げランキング: 572,816



